상세 컨텐츠
본문
나의 첫 블로그 소재이자 나의 현재 관심사는 골머리 아픈 프랙탈 fractal과 이를 응용한 다중프랙탈 분석 multifractal analysis이다. 아마 당분간 다루게 될 복잡계 이론의 이론적 토대가 되어줄 것으로 보인다. 이번 포스트는 내가 입문하는 과정을 기록하고 있으므로, 일반인들도 이해할 수 있도록 수학적 표현은 최대한 배제하려고 노력했다. 하지만 가끔 본질을 건드리는 부분에 대해선 잠시 언급하고 넘어가도록 할 것이기에, 수학 알러지 있으신 분들껜 미리 양해를 구한다.
용어 설명
해석학: 미적분학이 형식화된 것으로, 미적분학의 이론적 부분들을 수학적으로 정리한 학문.
유클리드 기하학: 특정 공리들(사실이라고 무조건 가정하는 사실들)을 중심으로 구성되는 도형에 대한 학문. 흔히 우리가 알고 있는 삼각형과 사각형, 정육면체, 점, 직선 등과 같은 도형에 대한 내용은 거의 모두 유클리드 기하학에서 기원한다.
수치해석: 해석학(혹은 미적분학)의 결과물의 수치를 최대한 정확히 측정하기 위한 방법론들을 모은 학문.
할선: 어떤 곡선을 뚫고 지나가는 직선. 해석학에선 곡선이 특정 조건을 만족할 때, 할선과 곡선과의 두 접점 사이의 거리가 0에 무한히 가까워질 때의 할선 기울기가 가까워지는 값을 특정 점의 접선의 기울기로 간주한다.
접선: 어떤 곡선에 접하는 직선. 해석학에선 그 기울기를 직접 구하는 것이 불가능한 것으로 간주하고, 할선을 통해 간접적으로 구한다.
측도: 우리가 무엇인가를 재거나 세는 행위를 수학적으로 추상화한 것.
참고사항
Fractal은 한국어로 프랙탈이라고 불리기도 하고, 프랙털이라고 불리기도 한다. 보통은 프랙탈이라고 잘 알려져 있고 앞으로의 포스트에서도 프랙탈이라고 지칭하겠지만, 프랙털이라는 용어도 사용됨을 미리 알리고자 한다.
해안선 길이 구하기와 해석학
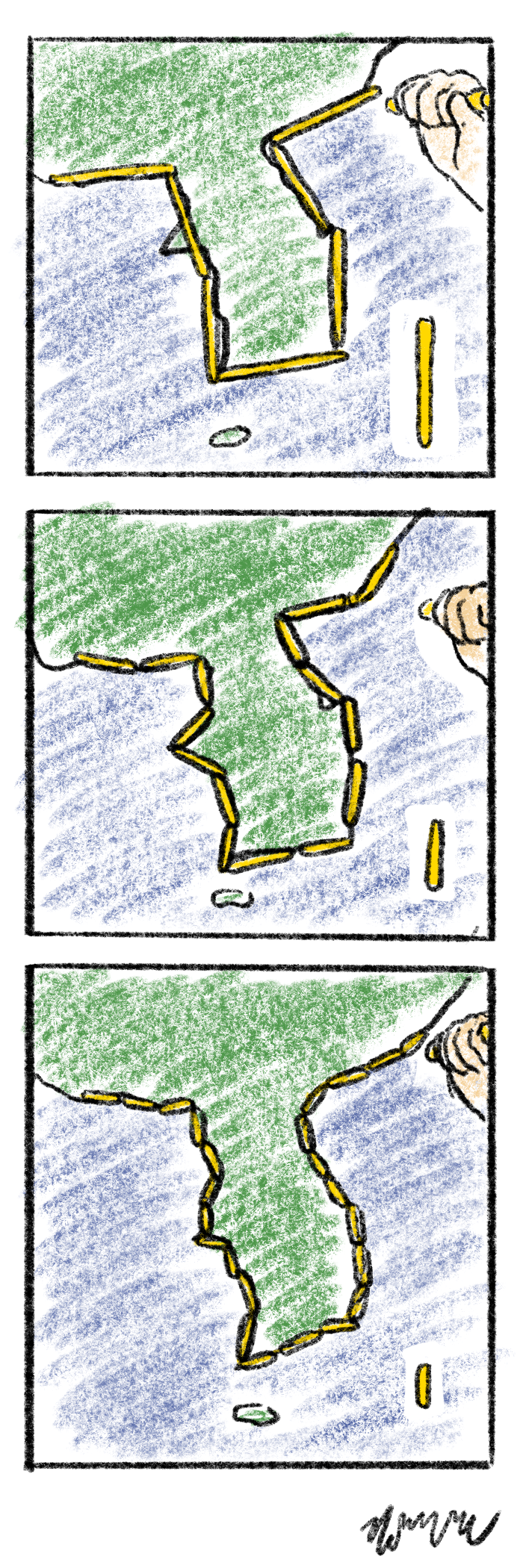
프랙탈은 그 이름에서 알 수 있듯이 무언가 쪼개거나 나누는 것과 관련이 있기는 하지만, 이름만으로는 그 정확한 본질에 대해서 바로 이야기하기엔 많은 이야기를 건너뛰어야 한다. 그래서, 처음으로 접하는 프랙탈을 이해하기 위해 프랙탈의 가장 익숙한 예시인 해안선에 대해서 이야기를 해보자.
우리가 지구본에서 보는 한반도는 중국과 일본 사이에 있는 비교적 조그만한 반도이다. 만약 어떤 호기심 많은 아이가 한반도의 둘레를 재고 싶으면, 아마 조그만한 자를 가져와서 커다란 지구본의 한반도 주위를 조금씩 대어보며 길이를 더할 것이다. 조금 더 똑똑한 아이는 실을 이용할지도 모른다. 어찌되었건 대부분의 '어른'들은 이런 자를 대는 행동이 바보같다고 생각하겠지만, 사실 이 아이들이 지금 하고 있는 행동은 수치해석 numerical analysis이라 부르는 아주 세련된 분야에서 하고자 하는 활동을 (다소 원시적이지만) 재현하는, 꽤 그럴듯한 행동이다. 예를 들어 자를 재어 보는 아이의 행동이 본질적으로 무엇을 하는 행동인지를 생각해 보자. 아이는 그냥 자를 아무렇게나 가져다 대는 것이 아니라, 자신이 잴 수 있는 가장 작은 단위의 길이에서 해안선의 평균적 각도를 어림한 후 그 단위만큼의 길이를 누적하여 더하는 것이다. 이 각도 어림은 해석학에서 할선 secant line을 찾으려 하는 것과 동일하다. 상식적으로, 만약 아이가 재는 자를 작은 것을 선택할수록, 이 자의 길이는 그 자가 뚫고 지나가는 해안선의 길이보다 조금 작지만 그래도 점점 근접하게 된다. 해석학적 관점에 따르면, 미분가능한(혹은 여기선 뾰족하게 튀어나오거나 끊어진 부분 없이 부드러운) 곡선은 유한한 기울기를 가지고 있고, 모든 할선의 기울기는 특정 접선 tangent line의 기울기와 같으므로, 만약 한 미분가능한 곡선을 나누는 할선이 많아질수록 그 할선의 개수가 증가하는 양과 유한한 비율로 할선의 길이도 짧아지게 된다 된다. 약간 어렵게 말했지만 간단히 말해, 해안선은 아주 가까이서 보면 부드럽게 연결되어 있으니, 아무리 자를 짧게 만들어서 엄청나게 많은 수의 길이를 더해야 하더라도, 그만큼 자의 길이도 엄청 작아지기 때문에 결국 길이는 하나의 수로 근사되게 된다는 것이다. 즉, 우리는 이 방법을 통해 해안선의 길이를 어느 정도의 정확도로 구할 수가 있는 식의 논리이다.
하지만, 정말로 가능할까?
해안선 길이 구하기의 현실

이 해안선 길이 구하기 문제에 대해서 수학자 망델브로 Mandelbrot가 한 이야기가 있다. 만약 위의 방법대로 자의 길이를 줄여가며 잰다고 생각해 보자. 문제점은 자의 길이를 줄이면서 시작된다. 만약 자의 길이를 줄인다면 더 정확한 측정을 위해 지도를 확대해야 하는데, 그러면 멀리선 보이지 않았던 울퉁불퉁한 해안선이 보일 것이다. 그러면 다시 그에 맞춰서 자의 길이를 더해야 한다. 또 다시 자의 길이를 줄이면 더 복잡한 해안선이 나오게 된다. 이렇게 되면 자의 길이가 줄어드는 것에 비해 필요한 자의 개수는 훨씬 더 많아지게 된다. 예시를 통해 잠시 살펴보자. 어떤 해안선을 재기 위해서 3개의 자가 필요했다. 그리고 자의 크기를 2배로 줄이고 해안선을 가로세로 2배로 확대했다. 그런데, 하나의 자로 해결되던 해안선이 확대하고 보니 이전과 같이 복잡한 패턴이 또 나타난 것이다. 그래서 동일한 해안선에 대해 이전의 자 한 개에 대해 절반짜리 자 2개가 아닌 이전 해안선처럼 3개의 절반짜리 자가 더 필요해졌다. 이렇게 되면 3개의 1짜리 자마다 3개의 1/2짜리 자가 생기는 것이므로, 이전에 3이었던 해안선이 4.5가 된다. 실제 해안선에서 자가 줄어들수록 얼마나 해안선이 길어질지는 정확히는 모르지만 확실한 건 자의 길이를 줄이면 해안선의 길이는 계속 큰 폭으로 늘어나기만 할 것이다.
이 문제에 대해서 이런 식으로 생각해보면 뭔가 이상하다. 상식적으로, 길이의 척도를 절반으로 줄이면 곡선의 길이는 2배가 된다. 왜냐하면 길이는 그대로 있고 이전 척도에 비해 새로운 척도로 계산하면 새로운 척도는 같은 길이에 대해 2배 더 많이 들어가기 때문이다. 비슷하게, 동일한 척도의 변화에 사각형의 넓이는 4배가 된다. 그 이유 역시 유사하게 넓이는 그대로 있지만 넓이는 재는 척도는 길이를 재는 척도의 제곱으로 계산되고, 그 길이의 척도가 절반이 되었으니 그의 제곱인 1/4배만큼 줄어든 척도 때문이다. 그런데, 위의 예시로 든 해안선을 보면, 척도를 절반으로 줄이면 3개의 자마다 3개의 자가 생기므로, 새로운 절반짜리 자는 3*3=9개로 늘어난다. 즉, 3배로 증가하는 것이다. 그러니 이 곡선은 일반적인 1차원 곡선처럼 2배로 늘어나는 것도 아니요, 2차원 평면처럼 4배로 늘어나는 것도 아니다. 그야말로 두 차원 사이에서 아슬아슬한 줄타기를 하고 있는 셈이다.
프랙탈로서의 해안선
이러한 해안선은 앞서 말했듯이 확대해서 보면 축소했을 때와 유사한 패턴이 다시 반복되고 있는 경우가 많다. 수학적으로 이러한 형태의 도형은 기존 수학에서의 두 가지 정도의 중대한 모순점과 한 가지의 중요한 사실을 품고 있다. 두 모순점은 각각 기존의 해석학과 유클리드 기하학에서 나타난다. 먼저, 해석학(더 구체적으로는 실해석학)의 전제를 받아들이고 수치해석적 방법으로 해안선과 같은 곡선의 길이를 잴려고 하면, 아무리 미분가능하더라도 하나의 고정된 길이로 수렴하지 않을 수 있다. 해석학의 관점에선 자의 크기를 줄일수록 점점 그 측정값은 하나의 값으로 가까워져야 하는데, 해안선과 같은 경우엔 자의 크기를 줄일수록 오히려 길이의 변화량이 계속 커지기만 한다. 해석학의 아이디어와 해안선의 실제 길이 간의 괴리는 이상적 측정 행위와 사실상 측정하는 행위 그 자체, 즉 기존의 곡선에 관한 측도 measure 에 대한 근본적 문제점을 꼬집는 것이다. 이것과 유사한 맥락으로, 유클리드 기하학의 전제와 다르게 확대와 축소의 관점에서 동적인 도형이 존재하는 점도 모순점 중 하나이다. 무슨 말인지 좀 더 풀어서 이해해 보자. 유클리드 기하학에선 어떤 곡선의 길이를 안다면 그 곡선을 확대하여도 그 곡선의 길이를 바로 알 수 있다. 곡선을 확대해봤자 곡선의 길이는 '고정'되어 있기 때문에 척도가 어떻게 바뀌었는지만 보면 정답을 알 수 있기 때문이다. 하지만 해안선은 다르다. 해안선을 확대할수록 계속 복잡한 패턴의 곡선이 새롭게 나타난다. 그 패턴에 따라 곡선의 길이를 재계산하면, 척도가 감소하는 배수에 비해 길이값는 더욱 가파르게 커진다. 즉, 보존될 줄 알았던 길이가 보존되질 못하는 것이다.
이러한 모순점들은 모두 무언가를 측정하는 측도와 연관이 되어 있으며, 이런 공통점은 곧 우리가 잘못된 '재는 방식'을 사용함을 알 수 있다. 이런 문제점은 마치 우리가 길이를 가지고 2차원 도형을 잴려는 것과 유사하다. 사각형의 '길이'를 재기 위해 사각형을 조금씩 잘라 길이를 조금씩 채워가봤자 영원히 우리는 사각형의 '길이'를 잴 수 없다. 사실 해안선의 길이를 재는 것은 가능하다고 생각하고 사각형의 길이를 재는 건 불가능하다고 우리가 생각한 이유는 단순하다. 넓이와 길이, 즉 2차원과 1차원은 딱 봐도 구분이 되지만, 해안선은 그냥 보기엔 1차원 같기 때문이다. 그러기에 망델브로와 같은 독특한 수학자들의 생각이 없었더라면, 우리는 아직도 해안선의 길이를 안다고 자신했을 것이다. 망델브로는 우리가 해안선의 길이를 '길이'로 잴 수 없음에 주목했다. 그는 우리가 사각형의 길이를 잴 수 없는 이유가 사각형이 1차원보다 높기 때문이라면, 해안선 또한 (이상하게도) 1차원보다 높을 것이라고 생각했다. 이런 식의 차원에 대한 접근을 제시하며, 망델브로는 앞서 우리가 같이 이야기한 길이 척도의 변화 배수와 도형 특성값의 변화 배수를 통해 구할 수 있는 하우스도르프 차원 Hausdorff dimension을 통해 해안선과 같은 도형들이 가진 '차원'을 짐작할 수 있게 했다. 그는 0이나 1, 2 등의 정수의 차원을 가지지 않은 이러한 도형들에게 '프랙탈'이라는 이름을 붙여주였다. 비정수 차원의 도형이라는 파격적인 아이디어 때문인지, 프랙탈 이론이 태동하던 시기엔 프랙탈은 현실적이지 않은 허상의 도형이라고 여겨졌다. 그렇지만 시간이 지나며 나무의 가지, 인간의 폐, 음악, 주식시장 등 자연과 인간 사회 속에서 프랙탈 구조가 발견되기 시작했다. 이후 프랙탈 이론과 혼돈 이론 간의 연관 관계가 발견되며, 프랙탈 이론은 복잡성을 설명하는 도구로서 다양한 분야에 적용되기 시작했다.
다음 이야기 | 차원 이론 dimension theory와 프랙탈 차원 구하기
Reference
1) "‘들쭉날쭉’ 해안선, 길이도 ‘들쑥날쑥’… 초미세 잣대로 잰다면 ‘∞’로 늘어나", 문화일보, last modified Mar 9, 2016, accessed Nov 22, 2020, www.munhwa.com/news/view.html?no=2016030901032403000001
‘들쭉날쭉’ 해안선, 길이도 ‘들쑥날쑥’… 초미세 잣대로 잰다면 ‘∞’로 늘어나
김범준의 과학 이야기 - ⑪ 우리나라 해안선 길이는?한반도는 북쪽을 제외한 동, 서, 남, 세 방향이 모두 바다..
www.munhwa.com
2) Lopes, R., & Betrouni, N. (2009). Fractal and multifractal analysis: a review. Medical image analysis, 13(4), 634-649.
3) Pearse, E. (2005). An introduction to dimension theory and fractal geometry: fractal dimensions and measures. URL: http://pi. math. cornell. edu/erin/docs/dimension. pdf.
4) 윤영수, & 채승병. (2005). 복잡계 개론. 서울: 삼성경제연구소.
5) Glendinning, Paul. (2017). 수학. 파주 :아르테 :arte :북이십일 .
Powered by Department of Mathematics, Wissen Society
페이스북 페이지 | www.facebook.com/wissenMath
오류/오타 신고 | 카카오톡채널 cellhelp
HyeonJun Kim © 2020 All Rights Reserved